Sorry, only in Dutch at the moment
een mauerwerkvorsprung probleem in de 21e eeuw
In 2007 kregen wij de opdracht om bovenop een bestaand kinderdagverblijf, daar er geen plek meer was op de grond, een nieuwe buitenschoolse opvang te ontwerpen met twee groepen van ieder twintig kinderen. Aangezien er behalve de 3,5 m2 per kind intern ook nog 4 m2 buitenspeelruimte per kind nodig was, lag het voor de hand een nieuw dek op het dak van het bestaande gebouw te maken dat als speelterrein kon dienen. Op dat dek twee paviljoens van zo'n kleine 100 m2 elk. Zeer tegen onze gewoonte in hebben we deze paviljoens vormgegeven als onregelmatige kristallijnen 'Mario Merz'-achtige iglo's om op die manier een contrast te maken met het orthogonale jaren-zeventig schooltje en het horizontale nieuwe dek.

We waren van mening dat deze onregelmatige uit driehoeken opgebouwde volumes zelfdragend moesten zijn. Dit omdat de voorbeelden waarbij dit soort vormgeving slechts een decor is dat met veel onzichtbaar stutwerk overeind moet worden gehouden te talrijk worden. Met behulp van constructeur Paul Lagendijk van Aronsohn Constructies en het Japanse programma Pepakura, waarmee je razendsnel bouwplaten kan printen van 3D modellen uit bijvoorbeeld SketchUp, hebben we zeer nauwkeurig de vorm van de paviljoens kunnen bepalen. Zodanig dat ze op het dek pasten, de stedebouwkundige situatie articuleerden, genoeg vrije interessante m2 hadden voor twintig kinderen, niet in zouden storten en ook nog eens aan onze esthetische eisen voldeden. Het bleek niet eenvoudig om ons theoretische computermodel met dikte nul voldoende stijf en sterk te krijgen. Met name de tweede, derde en meer, orde-effecten bleken soms desastreuze gevolgen te hebben voor de constructie, daar waar je die niet verwachtte. Maar dankzij een fantastische trial-and-error samenwerking met de constructeur hadden we uiteindelijk alles onder controle.
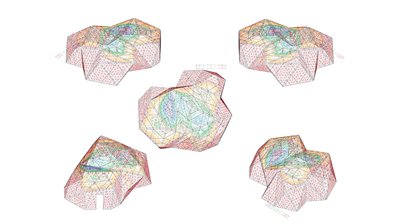
Het maken van de bestektekeningen voor de paviljoens leek ons weliswaar veel werk, maar in wezen een fluitje van een cent. Een simpele bewerking van ons dikte-nulmodel met wat in AutoCad Offset heet, zou moeten volstaan om vervolgens alle 36 panelen één voor één in 2D uit te tekenen, zodat de timmerfabriek daarvan simpele goedkope houtskeletbouwpanelen kon maken. Groot was onze verbazing toen dat helemaal niet zo eenvoudig bleek te zijn. Toen we het model een dikte hadden gegeven, bleken de hoekpunten zich te gedragen als een ontploft sterrenstelsel in plaats van de keurige piramides met drie tot acht vlakken.

Nog afgezien van de vorm- en bouwtechnische aspecten, was dit vooral zorgelijk omdat het oorspronkelijke hoekpunt niet meer bestond. Het was opgelost in een wolk van punten met een doorsnede van soms wel veertig centimeter. En dat terwijl tijdens het ontwerpen ervan was gebleken dat het verplaatsen van een hoekpunt over slechts dertig centimeter soms het verschil betekende tussen instorten of niet. We hadden dus een groot probleem. We begrepen niet wat er gebeurde, konden het niet in 2D tekenen en het was maar de vraag of onze paviljoens nog zouden blijven staan.
De wereld van parametrische geometrieën
Gelukkig lag het project net even stil vanwege bezwaren van de buren in een artikel 19 en kwamen we Axel Kilian tegen, mede auteur van het boek Architectural Geometry en op dat moment net in dienst bij de TUD. Hij wist ons te vertellen dat ons probleem in zijn vakgebied sinds een jaar een klassieker is en introduceerde ons in de wereld van parametrische geometrieën.
De positie van het theoretische computermodel met dikte nul was gekozen in het midden van de constructie. Voor de hand liggende oplossingen om het model toch dikte te kunnen geven, waren om bijvoorbeeld alleen de binnenkant of alleen de buitenkant kloppend te maken. Behalve dat we beide kanten kloppend en gesloten wilden hebben, was dat ook geen optie omdat we dan helemaal opnieuw konden beginnen met ontwerpen. Anders zou het gebouw te groot of te klein worden. Ook simpele bewerkingen, zoals alles naar één of twee punten offsetten, bleken te grote dikteverschillen in de vlakken op te leveren.
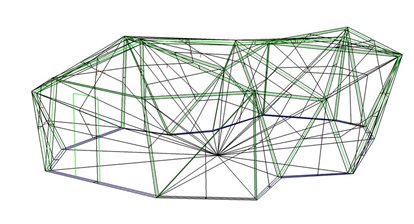
We besloten het fundamenteler aan te pakken en subsidie voor een onderzoek aan te vragen bij het Stimuleringsfonds. Die we gelukkig kregen.
Helmut Pottmann heeft in 2006 gepubliceerd2 hoe je met behulp van een kegel een 'normale' piramide met vier vlakken offsetbaar kon maken. Het was echter de vraag of dat ook voor piramides met meer vlakken zou gelden en voor piramides met een inham of deuk, zoals wij ze genoemd hebben. Zo systematisch mogelijk hebben we een soort 'periodiek systeem' voor piramides opgezet, waaruit onder andere bleek dat het mogelijk is om piramides tot wel acht vlakken offsetbaar te maken. Tevens bleek dat het grondvlak van offsetbare piramides met een oneven aantal vlakken een vlak is en dat dat bij een even aantal vlakken niet het geval hoeft te zijn. Ook bleek dat piramides met deuken wel degelijk offsetbaar zijn, mits de (verlengde) raaklijn raakt aan de grondcirkel van de kegel. Op het moment dat het diepste punt ven een deuk samenvalt of voorbij de top van de kegel terecht komt, kan het echter niet.
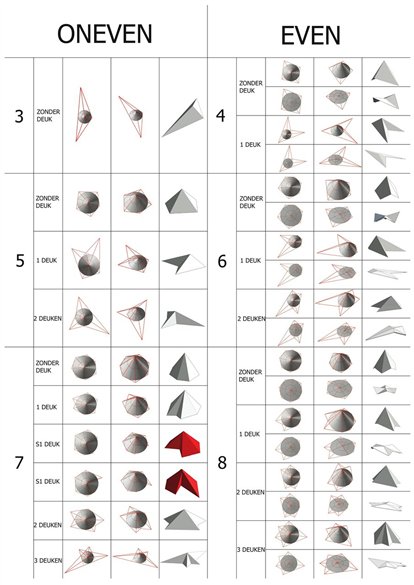
Na deze exercitie en haar conclusies was het de vraag hoe we de aan elkaar gekoppelde piramides allemaal samen tegelijk offsetbaar konden maken. Dat is lastig, daar een verschuiving van één vlak van één piramide onmiddellijk een verschuiving van datzelfde vlak in tenminste twee andere piramides tot gevolg heeft. Een oneindige aanpassing van steeds opnieuw alle piramides ligt op de loer. Maar gelukkig zijn er wel een aantal constanten te benoemen waarin gevarieerd kan worden. Zoals: doorsnede van de basiscirkel van de kegel, hoogte van de kegel, hoek van de kegel. Maar na talloze pogingen met verschillende constanten en variabelen en zelfs een ellips als constante (een schuine doorsnede van een kegel, die als voordeel twee brandpunten heeft) moesten we concluderen dat dit een heilloze weg was.
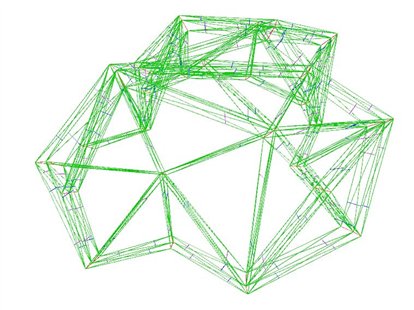
Iteratie leek het enige alternatief. Ofwel: het met heel veel botte rekenkracht terugrekenen van de afwijkingen naar iets dat verwaarloosbaar klein zou worden. Axel Kilian had inmiddels zijn zeer behulpzame wereldwijde netwerk ingeschakeld en op een gegeven moment werd er op verschillende plekken in de wereld zwaar gerekend aan de door ons ontworpen vorm.
Maar ook deze pogingen bleken vergeefs. Ondanks alle zeer inventieve en krachtige parametrische rekenmethodes bleven de vlakken in dikte teveel verschillen of waren de kopse kanten te veel getordeerd om in simpele houtskeletbouw te kunnen maken.
Inmiddels waren we een jaar verder, waren de bezwaren van de buren ongegrond verklaard en wenste de opdrachtgever aan te besteden. Wij zagen op dat moment geen andere uitweg dan om maar 'handmatig' in de computer in het 3D model de toppen van de piramides zodanig 'op te ruimen en schoon te maken' dat er een bouwbaar geheel van te maken viel. De 3D panelen van het model hebben we in Rhino één voor één neergeslagen en vervolgens in Vectorworks tot een 'normale' 2D bestek tekening gemaakt.
Inmiddels waren we echter zo wantrouwig geworden over ons eigen werk dat we besloten dit eerst te testen in een 1:10 schaal model van berkenmultiplex. De verbindingen hebben we gemaakt met supermagneten die op schaal eenzelfde trekkracht leveren als in werkelijkheid de draadeinden met kramplaten. Gelukkig bleek alles te kloppen en ook nog te blijven staan.
Een plug-in voor SketchUp?
De aanbesteding verliep voorspoedig. De paviljoens bleken nauwelijks duurder dan een 'normaal' hsb-gebouwtje. Het buitenspeeldek bleek
echter wel nogal prijzig. Daar kwam bij dat bso buitenspeelruimte nu opeens ook buiten het eigen terrein gevonden mocht worden. Hiermee verviel de noodzaak van het dek en de paviljoens en was het hele project van de baan. Het onderzoek liep nog even door en de belangrijkste conclusie is dat het verstandig is om vanaf het begin van het ontwerpproces rekening te houden met de offsetbaarheid van een vrije, onregelmatige vorm. Vooralsnog gaat dat het beste door de vlakken te laten raken aan bijvoorbeeld een bol. Die vlakken kunnen voor wat betreft de offsetbaarheid beter geen driehoeken zijn, ondanks de voor de hand liggende voordelen als stabiliteit en simpelheid, maar beter onregelmatige vierhoeken waarbij de hoekpunten in één vlak of op en cirkel liggen. Maar de belangrijkste aanbeveling is eenzelfde die ook al in Architectural Geometry wordt getrokken namelijk dat architecten zitten te springen om een optimalisatieroutine waarin onregelmatige meshes 'automatisch' als offsetbare vormen worden getekend. Wellicht dat de makers van SketchUp hier eens een plug-in voor kunnen bedenken.

Met dank aan:
Paul Lagendijk, Aronsohn constructies raadgevens ingenieurs bv; Axel Kilian, Princeton University; Hanna Läkk; Ralph Doggen; Gerry Bekhuis; Sarah van der Made; Martijn Stellingwerff TU Delft; Van Dik Hout; Henry Burgers; Het Stimuleringsfonds voor de Architectuur Rotterdam